SŁOWNIK MATEMATYCZNY
A B C D E F G H I J K L Ł M N O P R S Ś T U W V X Y Z Ż
SŁOWNIK MATEMATYCZNY - Ś
ściana : wielościan
Ślebodziński Władysław (1884-1972) : Matematyk polski,zajmował się głównie nowoczesną geometrią różniczkową
ślimak Pascala : Krzywa płaska, konchoida okręgu. Jeżeli we współrzędnych biegunowych okrąg ma równanie : r = a , to równanie ślimaka Pascala ma postać r=a cos Θ + b, we współrzędnych prostokątnych : (x2 + y2 - ax)2 = b2(x2+y2). Krzywą tą po raz pierwszy zajmował się Étienne Pascal, ojciec wielkiego matematyka. Kształt ślimaka Pascala zależy od stosunku b do a. Gdy b = a ślimak Pascala nazywamy kardioidą. Ślimak Pascala jest epicykloidą.
Śniadecki Jan (1756-1830) : Matematyk, astronom i filozof polski. Studiował w Krakowie, Getyndze i Paryżu. Od 1781 był profesorem matematyki i astronomii w Krakowie, od 1807 w Wilnie. W 1783 wydał swoje główne dzieło matematyczne pt. "Rachunku algebraicznego teoria przystosowana do linii krzywych", podręcznik algebry wyższej wraz z elementami geometrii analitycznej i trygonometrii. W 1817 ukazał się druga większa praca matematyczna Śniadeckiego "Trygonometria kulista analitycznie wyłożona". Śniadecki stworzył polską terminologię matematyczną, położył wielkie zasługi na polu popularyzacji i dydaktyki matematyki oraz organizacji życia naukowego.
średnia arytmetyczna SA liczba a1,a2,..,an : Iloraz ich sumy przez b średnia geometryczna SG liczb dodatnich a1,a2,...,an : Pierwiastek arytmetyczny stopnia n z ich iloczynu: średnia harmoniczna SH liczb dodatnich a1,a2,...,an : Odwrotność średniej arytmetycznej odwrotności tych liczb średnia kwadratowa SK liczb a1,a2 : Pierwiastek arytmetyczny ze średniej arytmetycznej ich kwadratów średnia proporcjonalna dwóch liczb dodatnich : Średnia geometryczna tych liczb średnia wartość : W rachunku prawdopodobieństwa to samo co wartość przeciętna średnica okręgu : okrąg średnica zbioru : Kres górny wzajemnych odległości elementów x i y zbioru Z będącego podzbiorem przestrzeni metrycznej Średnia zbioru oznaczana jest symbolem δ(X), Jeśli zbiór X jest kołem lub kulą, to średnia zbioru X jest długością średnicy w zwykłym sensie. Przestrzenie metryczne o średnicy skończonej nazywamy ograniczonymi średnice sprzężone : elipsa środek ciężkości trójkąta : środkowa środek jednokładności : jednokładność środek krzywizny : krzywizna środek obrotu : kąt obrotu środek odcinka : odcinek środek rzutów : rzut środek symetrii : symetria środkowa w trójkącie : Odcinek łączący wierzchołek trójkąta ze środkiem boku przeciwległego. Trójkąt ma trzy środkowe przecinające się w jednym punkcie S zwanym środkiem ciężkości trójkąta o współrzędnych xS = xA+xB+xC / 3 yS= yA+yB+yC (na płaszczyźnie).Środek ciężkości dzieli środkową na dwa odcinki; odcinek, którego jeden koniec jest wierzchołkiem trójkąta, jest dwa razy dłuższy od drugiej części środkowej. Odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i równy jest jego połowie. śruba mikrometryczna : mikrometr
W naukach doświadczalnych, gdy pomiar pewnej wielkości wykonywany jest kilkakrotnie, przyjmujemy jako miarę tej wielkości śrdenij arytmetycznej z wyników pomiarów, jako wartość najbardziej prawdopodobną.
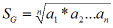
. Średnia geometryczna dwóch liczb może być łatwo wyznaczona konstrukcyjnie ,z uwagi na to ,że wysokość trójkąta prostokątnego poprowadzona z wierzchołka kąta prostego jest średnią geometryczną odcinków, na jakie dzieli ona przeciwprostokątną.
n/SH = 1/a1 + 1/a2+...+1/an. Okazuje się ,że średnia harmoniczna jest mniejsza od średniej geometrycznej, a więc także od średniej arytmetycznej tzn. SH ≤ SG ≤ SA
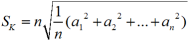
Średnia kwadratowa ma ważne znaczenie w teorii błędów